1. Tujuan [back]
Memahami rangkaian logika dengan menggunakan J-K Flip flop dengan clock, sebagai operasi penghitung riak biner.
2. Alat dan Bahan [back]
Alat dan bahan yang digunakan yaitu :
a. Negative edge triggered J-K flip-flops
b. clock
c. Logicstate
d. Logic probe
e. Gerbang NAND
3. Dasar Teori [back]
- Negative Edge-Triggered J-K flip-flops
Pada JK flip-flop dibuat jalur balik
dari masing-masing keluaran Q dan Q’ menuju gerbang masukan NAND, hal ini
tidak masalah karena gerbang NAND dapat memiliki lebih dari dua masukan.
Nama JK flip-flop diambil untuk membedakan dengan masukan pada SR
flip-flop karena ada perubahan ada perubahan jalur balik di atas. Secara umum
cara kerja JK flip-flop sama dengan SR flip-flop. Perbedaannya pada saat JK
bernilai 1 1 yang menyebabkan kondisi keluaran berubah (1 ke 0 dan 0 ke 1) atau
toggle.
JK flip-flop memiliki 2 masukan yang biasanya ditandai dengan huruf J dan
K. Jika J dan K berbeda maka keluaran Q akan sama dengan nilai J pada clock
berikutnya (next clock). Jika J dan K keduanya 0 maka tidak terjadi perubahan
apa-apa pada flip-flop. Jika J dan K keduanya 1 maka kondisi Q akan berubah dari
kondisi sebelumnya, Jika sebelumnya Q bernilai 0 maka akan bernilai 1 dan
sebaliknya.
Karakter JK flip-flop yang lebih pasti untuk semua kondisi maka flip-flop
ini yang banyak digunakan untuk membangun berbagai komponen register
seperti: register geser (shift register), pencacah biner (binary counter),
pendeteksian sekuensial (sequence detector) dan lain-lain.
Pada saat clock naik/bernilai 1 maka kondisi keluaran Q ditentukan oleh
masukan JK. Kondisi Set (keluaran bernilai 1) tercapai pada saat JK bernilai 10.
Kondisi Reset (keluaran bernilai 1) tercapai pada saat JK bernilai 01. Pada flip flop
JK tidak ada lagi kondisi pacu seperti pada flip-flop SR. Pada saat JK bernilai 11
maka nilai keluaran Q akan berubah-ubah (toggle) pada saat setiap clock -nya.
tabel kebenaran JK Flip flop
2. Clock (detak)
lock yaitu pulsa-pulsa periodik yang biasanya berbentuk bujur sangkar
(duty cycle 50%), seperti yang ditunjukkan pada gambar 16. SR Flip-Flop bekerja
secara asinkron. Nilai S dan R dapat berubah kapan saja dan dalam tempo yang
tidak bersamaan. Detak (clock) ditambahkan pada sisi masukan untuk menjaga
sinyal agar bekerja dalam tenggang tempo yang bersamaan.
Operasi-operasi yang terjadi di dalam sistem digital sinkron terjadi pada
waktu-waktu pulsa clock bertransisi dari 0 ke 1 atau dari 1 ke 0. Waktu-waktu
transisi ini ditunjukkan pada gambar 16. Transisi 0 ke 1 disebut sisi naik (rising
edge) atau sisi menuju positif, transisi dari 1-ke-0 disebut sisi jatuh (falling edge)
atau sisi menuju negatif.
Kendali ini membantu flip-flop lebih stabil. Clock ditambahkan sebelum
sinyal S dan R masuk ke dalam rangkaian flip-flop. Masing-masing sinyal masukan
di NAND-kan dengan clock. Pada saat clock bernilai 0, tidak ada perubahan sinyal
yang masuk ke dalam flip-flop.
3. Logicstate
untuk memberikan nilai logika 1 atau 0
4. Logicprobe
untuk menampilkan nilai keluaran, yang nilainya 0 atau 1.
5. Gerbang NAND
menampilan nilai inverter dari input gerbang AND.

Binary Ripple Counter
Pengoperasian penghitung riak biner dapat dijelaskan dengan bantuan penghitung tipikal jenis ini. Gambar 11.2 (a) menunjukkan penghitung riak empat-bit yang diimplementasikan dengan kabel flip-flop J-K negatif yang dipicu sebagai toggle flip-flop. Output dari flip-flop pertama mengumpankan input jam dari yang kedua, dan output dari flip-flop kedua mengumpankan input jam dari yang ketiga, output yang pada gilirannya memberi makan input jam dari flip-flop keempat. Output dari keempat flip-flop ditetapkan sebagai Q0 (LSB flip-flop), Q1, Q2 dan Q3 (MSB flip-flop). Gambar 11.2 (b) menunjukkan bentuk gelombang yang muncul pada keluaran Q0, Q1, Q2 dan Q3 saat sinyal clock melewati siklus pulsa pemicu yang berurutan. Fungsi penghitung sebagai berikut. Mari kita asumsikan bahwa semua flip flop pada awalnya dihapus ke kondisi '0'. Pada transisi TINGGI ke RENDAH dari pulsa jam pertama, Q0 beralih dari ‘0’ ke ‘1 ow karena tindakan bergantian. Karena flip flop yang digunakan adalah yang dipicu oleh negatif edge, transisi '0' ke '1' pada Q0 tidak memicu flip-flop FF1. FF1, bersama dengan FF2 dan FF3, tetap dalam kondisi '0'. Jadi, pada terjadinya transisi clock negative-going pertama, Q0 = 1, Q1 = 0, Q2 = 0 dan Q3 = 0. Pada transisi TINGGI ke RENDAH dari pulsa clock kedua, Q0 beralih lagi. Artinya, mulai dari ‘1’ hingga ‘0’. Transisi '1' ke '0' pada output Q0 memicu FF1, output Q1 yang berasal dari '0' ke ‘1’. Output Q2 dan Q3 tetap tidak terpengaruh. Oleh karena itu, segera setelah terjadinya transisi TINGGI ke RENDAH kedua dari sinyal clock, Q0 = 0, Q1 = 1, Q2 = 0 dan Q3 = 0. Pada baris yang sama, kita dapat menjelaskan status logika Q0, Q1 , Output Q2 dan Q3 segera setelah transisi jam berikutnya. Status logika output untuk 16 pertama transisi sinyal jam relevan (TINGGI ke RENDAH) dirangkum dalam Tabel 11.1. Dengan demikian, kita melihat bahwa penghitung melewati 16 keadaan yang berbeda dari 0000 ke 1111 dan kemudian, pada terjadinya transisi yang diinginkan dari pulsa clock keenambelas, ia me-reset ke keadaan asli 0000 dari tempat dimulainya. Secara umum, jika kita memiliki N flip flop, kita bisa menghitung pulsa 2N sebelum penghitung ulang ke keadaan awal. Kita juga bisa melihat dari gelombang Q0, Q1, Q2 dan Q3, seperti yang ditunjukkan pada Gambar 11.2 (b), bahwa frekuensi gelombang Q0, Q1, Q2 dan Q3 masing-masing adalah f / 2, f / 4, f / 8 dan f / 16. Di sini, f adalah frekuensi input jam. Ini menyiratkan bahwa penghitung jenis ini dapat digunakan sebagai sirkuit divide-by-2N, di mana N adalah jumlah flip flop dalam rantai penghitung. Faktanya, penghitung seperti itu menyediakan keluaran frekuensi-f dari f / 2N, f / 2N − 1, f / 2N − 2, f / 2N − 3,, f / 2 pada output Nth, (N −1) th, (N − 2) th, (N − 3) th,, flip flop pertama. Dalam kasus penghitung empat bit dari tipe yang ditunjukkan pada Gambar. 11.2 (a), output tersedia pada f / 2 dari output Q0, pada f / 4 dari output Q1, pada f / 8 dari output Q2 dan pada f / 16 dari output Q3. Dapat dicatat bahwa pembagian frekuensi adalah salah satu aplikasi utama penghitung.
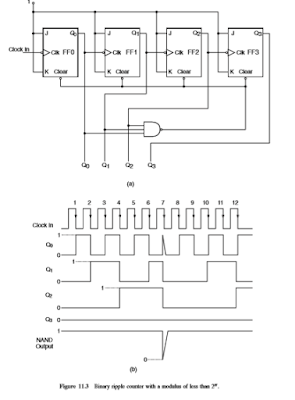
A. Binary Ripple Counters with a Modulus of Less than 2^N
Penghitung riak biner N-flip-flop dapat dimodifikasi, seperti yang akan kita lihat dalam paragraf berikut, untuk memiliki modulus lain kurang dari 2N dengan bantuan logika kombinasional sederhana yang terhubung secara eksternal.
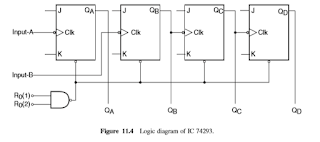
B. Ripple Counters in IC Form
Di bagian ini, kita akan melihat diagram logika internal penghitung riak biner yang umum dan melihat seberapa dekat arsitekturnya dengan penghitung riak yang dijelaskan di bagian sebelumnya. Mari kita pertimbangkan nomor tipe penghitung riak biner 74293. Ini adalah penghitung riak biner empat bit yang berisi empat flip-flop J-K master-slavetype dengan gating tambahan untuk menyediakan penghitung pembagian-oleh-2 dan penghitung MOD-8 tiga-tahap. Gambar 11.4 menunjukkan diagram logika internal penghitung ini. Untuk mendapatkan urutan biner penuh dari 16 status, output Q dari flip-flop LSB terhubung ke input B, yang merupakan input clock dari flip-flop berikutnya yang lebih tinggi. Pengaturan kemudian menjadi sama seperti yang ditunjukkan pada Gambar. 11.2 (a), dengan pengecualian gerbang NAND dua-input pada Gambar 11.4, yang telah dimasukkan di sini untuk menyediakan fitur-fitur pembersihan.
a. Fig. 11.2
Prinsip kerja :
Rangkaian akan aktif ketika logika input adalah 1. Ketika logika input 1 maka fungsi penghitung sebagai berikut. Mari kita asumsikan bahwa semua flip flop pada awalnya dihapus ke kondisi '0'. Pada transisi TINGGI ke RENDAH dari pulsa jam pertama, Q0 beralih dari ‘0’ ke ‘1 ow karena tindakan bergantian. Karena flip flop yang digunakan adalah yang dipicu oleh negatif edge, transisi '0' ke '1' pada Q0 tidak memicu flip-flop FF1. FF1, bersama dengan FF2 dan FF3, tetap dalam kondisi '0'. Jadi, pada terjadinya transisi clock negative-going pertama, Q0 = 1, Q1 = 0, Q2 = 0 dan Q3 = 0. Pada transisi TINGGI ke RENDAH dari pulsa clock kedua, Q0 beralih lagi. Artinya, mulai dari ‘1’ hingga ‘0’. Transisi '1' ke '0' pada output Q0 memicu FF1, output Q1 yang berasal dari '0' ke ‘1’. Output Q2 dan Q3 tetap tidak terpengaruh. Oleh karena itu, segera setelah terjadinya transisi TINGGI ke RENDAH kedua dari sinyal clock, Q0 = 0, Q1 = 1, Q2 = 0 dan Q3 = 0. Pada baris yang sama, kita dapat menjelaskan status logika Q0, Q1 , Output Q2 dan Q3 segera setelah transisi jam berikutnya. Status logika output untuk 16 pertama transisi sinyal jam relevan (TINGGI ke RENDAH) dirangkum dalam Tabel 11.1. Dengan demikian, kita melihat bahwa penghitung melewati 16 keadaan yang berbeda dari 0000 ke 1111 dan kemudian, pada terjadinya transisi yang diinginkan dari pulsa clock keenambelas, ia me-reset ke keadaan asli 0000 dari tempat dimulainya. Hal ini sesuai dengan tabel kebenaran.
b. Fig. 11.3
Prinsip Kerja :
Rangkaian ini menggunakan J-K flip-flop dengan tidak aktifLOWsinkronkan CLEARinput. NANDmembukintidakmenentukanoutput yang terhubung dengan input CLEAR dari keempat flip-flop. Input ke gerbang NAND tiga input ini berasal dari output Q dari flip-flop FF0, FF1 dan FF2. Jika kita mengabaikan gerbang NAND untuk beberapa waktu, penghitung ini akan melalui urutan biner alami dari 0000 hingga 1111. Tetapi itu tidak terjadi dalam pengaturan saat ini. Penghitung mulai menghitung dari 0000 ke penghitungan akhir 1111. Penghitung terus menghitung selama input CLEAR asinkron dari flip flop berbeda tidak aktif. Artinya, output gerbang NAND adalah TINGGI. Ini adalah kasus sampai penghitung mencapai 0110. Dengan pulsa jam ketujuh ia cenderung pergi ke 0111, yang membuat semua gerbang NAND input TINGGI, memaksa outputnya ke RENDAH. Transisi TINGGI ke RENDAH ini pada output gerbang NAND membersihkan semua output flip-flop ke keadaan logika '0', sehingga tidak memungkinkan penghitung untuk diselesaikan pada 0111. Dari pulsa jam kedelapan dan seterusnya, penghitung mengulangi urutannya. Penghitung dengan demikian selalu dihitung dari 0000 hingga 0110 dan kembali ke 0000. Sembilan negara sisanya, yang meliputi 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110 dan 1111 dilewati, dengan hasil bahwa kita mendapatkan Penghitung MOD-7. Gambar 11.3 (b) menunjukkan bentuk gelombang waktu untuk penghitung ini. Dengan memilih input NAND yang sesuai, seseorang dapat memperoleh penghitung dengan nomor MOD apa pun yang kurang dari 16. Pemeriksaan bentuk gelombang waktu juga mengungkapkan bahwa frekuensi output Q2 adalah 1/7 dari frekuensi clock input. Bentuk gelombang pada output Q2, bagaimanapun, tidak simetris seperti yang akan terjadi jika penghitung akan melalui urutan biner penuh. Output Q3 tetap dalam kondisi logika RENDAH. Diharapkan demikian karena penghitung MOD-7 membutuhkan minimal tiga flip flop. Itulah sebabnya flip-flop keempat, yang seharusnya beralih pada transisi TINGGI ke RENDAH dari pulsa clock kedelapan, dan pada setiap pulsa kedelapan berturut-turut sesudahnya, tidak pernah sampai ke tahap itu. Penghitung dihapus pada pulsa clock ketujuh dan setiap pulsa clock ketujuh berturut-turut sesudahnya. Sebagai ilustrasi lain, jika gerbang NAND yang digunakan dalam pengaturan penghitung pada Gambar 11.3 (a) adalah NAND dua-input dan inputnya berasal dari output Q1 dan Q3, penghitung akan melewati 0000 hingga 1001 dan kemudian mengatur ulang ke 0000 lagi, karena, saat penghitung cenderung beralih dari kondisi 1001 ke kondisi 1010, gerbang NAND beralih dari status '1' ke status '0', membersihkan semua flip flop ke status '0'.
c. Fig. 11.4
Penghitung dihitung dalam urutan alami dari 0000 hingga 1011.
Saat penghitung masuk ke 1100, output NAND pergi ke keadaan logika '0' dan segera membersihkan penghitung ke keadaan 0000.
Dengan demikian, penghitung tidak dapat tetap berada di negara bagian 1100. Hanya memiliki 12 status stabil dari 0000 hingga 1011. Oleh karena itu, modulus penghitung = 12.
Output Q3 adalah frekuensi input jam dibagi 12.
Oleh karena itu, frekuensi gelombang output Q3 = 1.2 × 103/12 = 100 kHz
d. Example 11.3 (fig. 11.5)
soal : Lihat counter riak biner dari Gambar 11.5. Tentukan modulus konter dan juga frekuensi output Q3 flip-flop.
prinsip kerja :
Ketika input berlogika 1, maka sepanjang waktu gelombang pada flip flop JK 1 akan menggambarkan sinyal normal, sedangkan pada flip flop 2, 3, 4 terhubung ke gerbang NAND,
e. Example 11.4 (fig. 11.6)
soal : Rancang penghitung riak biner yang menghitung 000 dan 111 dan lompati enam status yang tersisa, yaitu, 001, 010, 011, 100, 101 dan 110. Gunakan flip flop JK yang dipicu oleh tepi negatif yang dipicu oleh tepi rendah PRESET dan CLEAR yang aktif input. Juga, gambarkan bentuk gelombang pewaktuan dan tentukan frekuensi dari keluaran flip-flop yang berbeda untuk frekuensi clock yang diberikan, fc.
Prinsip kerja :
Penghitung diharuskan untuk pergi ke negara bagian 111 dari negara bagian 000 dengan transisi jam relevan pertama. Transisi kedua membawanya kembali ke status 000. Yaitu, tiga flip flop beralih dari keadaan logika '0' ke keadaan logika '1' dengan setiap transisi jam bernomor ganjil, dan juga tiga flip flop beralih dari keadaan logika '1' ke keadaan logika '0' dengan setiap transisi jam genap. Gambar 11.6 (a) menunjukkan pengaturan. Input PRESET dari ketiga flip-flop telah dikaitkan dengan output NAND yang inputnya QA QB dan QC Setiap kali penghitung berada dalam status 000 dan clock, output NAND sejenak beralih dari status logika '1' ke status keadaan logika '0', dengan demikian mengatur QA QB dan keluaran QC ke keadaan logika '1'. Bentuk gelombang QA, QB dan QC identik, dan masing-masing memiliki frekuensi fc / 2, di mana fc adalah frekuensi clock.
f. Example 11.5 ( fig. 11.7)
soal : Lihat pengaturan penghitung riak biner dari Gambar 11.7. Tulis urutan hitungannya jika awalnya dalam kondisi 0000. Juga menggambar gelombang waktu.
Prinsip Kerja :
Penghitung awalnya dalam kondisi 0000. Dengan pulsa jam pertama, Q0 beralih dari '0' ke '1', yang berarti Q0 beralih dari '1' ke '0'. Karena Q0 di sini memasukkan input clock dari flip-flop berikutnya, FF1 flip-flop juga beralih. Jadi, Q1 beralih dari '0' ke '1'. Karena sandal jepit FF2 dan FF3 juga dibukukan dari keluaran pelengkap sandal jepit mereka sebelumnya, mereka juga beralih. Dengan demikian, penghitung bergerak dari kondisi 0000 ke kondisi 1111 dengan pulsa clock pertama. Dengan pulsa clock kedua, Q0 beralih lagi, tetapi flip-flop lainnya tetap tidak terpengaruh karena alasan yang jelas dan penghitung berada dalam kondisi 1110. Dengan pulsa clock berikutnya, penghitung terus menghitung ke bawah oleh satu LSB pada satu waktu sampai mencapai 0000 lagi, setelah itu proses berulang. Urutan penghitungan diberikan sebagai 0000, 1111, 1110, 1101.1100, 1011, 1010, 1001, 1000, 0111, 0110, 0101, 0100, 0011, 0010, 0001 dan 0000. Bentuk waktu ditunjukkan pada Gambar 11.8. Jadi, kami memiliki penghitung empat bit yang diperhitungkan dalam urutan terbalik, dimulai dengan penghitungan maksimum. Ini adalah penghitung BAWAH.
Fig. 11.2
Fig. 11.4
Fig. 11.5
Fig. 11.6
Fig. 11.7
Rangkaian simulasi
Video
HTML : download
Data sheet JK Flip Flop : download
Data sheet NAND gate : download

















Tidak ada komentar:
Posting Komentar